2017-10-11
Back to listIn this blog post, we introduce a new technique to train deep learning models titled, “Mixed Precision Training”. In this joint work with NVIDIA, we train deep learning models using IEEE half precision floating point numbers. Most deep learning models today are trained using 32 bit single precision floating point numbers (FP32). Through this technique, we can reduce the memory needed for training deep learning models using 16 bit floating point numbers (FP16). In addition, we can take advantage of faster compute units available in hardware processors.
Deep learning models consist of various layers including fully connected layers, convolution layers, and recurrent layers. Each of these layers can be implemented using General Matrix Multiply (GEMM) operations. The GEMM operation takes up the majority of the compute during training. As shown in the figure below, the GEMM operation can be split into several multiplication operations followed by an addition.
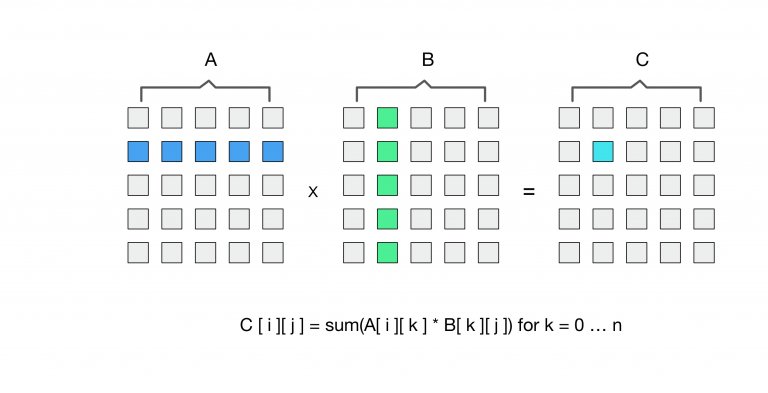
Figure 1: Matrix Multiplication [1]
When using FP16 for representing numbers in a neural network, the input matrices to the GEMM operation consist of 16 bit numbers. We need hardware that can perform the multiplication using 16 bit compute, but the addition needs to be performed using 32 bit compute and storage. It becomes very difficult to train large deep learning models using less than 32 bits for the addition operation.
In addition to this hardware support, we also introduce some changes to the training pipeline. Inputs, weights, gradients and activations in the models are represented in FP16 format. Some models don’t converge to the same accuracy as the single-precision baseline by simply changing the storage format. Half-precision numbers have limited range compared to FP32 numbers. In order to solve this challenge, we propose two techniques. Firstly, we maintain a master copy of the weights in FP32 format. FP16 weights are used for forward and backward propagation. The gradient updates from the optimizer are added into the master FP32 copy. This FP32 copy is rounded down to FP16, which is used during training. This process is repeated on every training iteration until the model converges and allows us to recover the loss in accuracy. By using the FP16 weights in training, we can take advantage of faster hardware for FP16 numbers. The figure below shows a mixed precision training iteration.
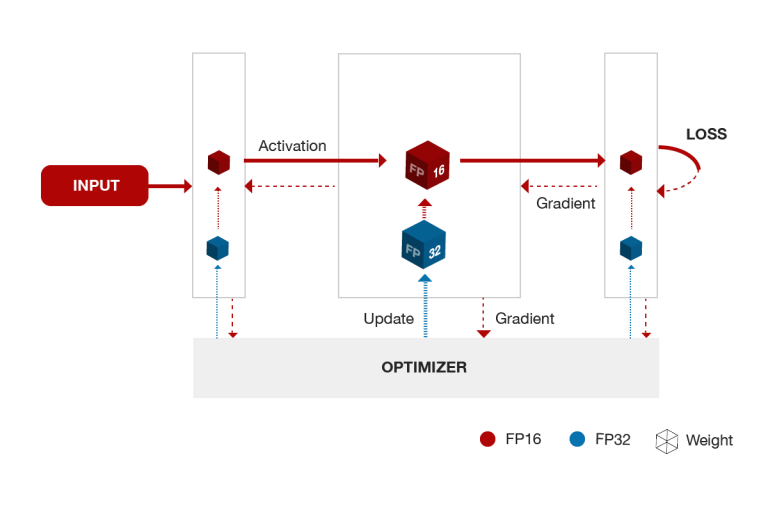
Figure 2: Mixed precision training for deep learning models.
Secondly, we introduce a technique called loss-scaling that allows us to recover some of the small valued gradients. During training, some weight gradients have very small exponents that become zero in FP16 format. To overcome this problem, we scale the loss using a scaling factor at the start of back-propagation. Through the chain-rule, the gradients are also scaled up and become representable in FP16. The gradients do need to be scaled down before the update is applied to the weights. Loss-scaling is necessary to recover the loss in accuracy for some models. More details regarding both these techniques can be found in our paper.
Using this approach, we are able to train the DeepSpeech 2 model using FP16 numbers. For both English and Mandarin models/datasets, we can match the accuracy of the FP32 models. We use the same hyper-parameters and model architecture for the mixed precision training experiments. The full set of experiments and results are available in the paper.
We can reduce the memory requirements for training deep learning models by nearly 2x using FP16 format for weights, activations and gradients. This reduced memory footprint allows us to use half the number of processors for training these models, effectively doubling the cluster size. Additionally, peak performance for FP16 arithmetic (described above) is usually a lot higher than single precision compute. This technique enables us to take advantage of the faster compute units available for FP16 numbers.
Results for training convolution neural networks on the ImageNet dataset using mixed precision training are available at Nvidia’s blog.
For a more details regarding mixed precision training and the full set of results and experiments, please refer to our paper on arXiv.
By Sharan Narang, Systems Researcher, Baidu Research
1. Image credit: https://insidehpc.com/2016/01/heterogeneous-streams/